获取质数算法：埃拉托斯特尼筛法

埃拉托斯特尼筛法

本算法的核心思想是：给出要筛选数值的范围 n，找出 √𝑛 以内的素数 p1, p2…, p𝑘。先用 2 去筛，即把 2 留下，把 2 的倍数剔除掉；再用下一个素数，也就是 3 筛，把 3 留下，把 3 的倍数剔除掉；接下去用下一个素数 5 筛，把 5 留下，把 5 的倍数剔除掉；不断重复下去……

如下图所示：

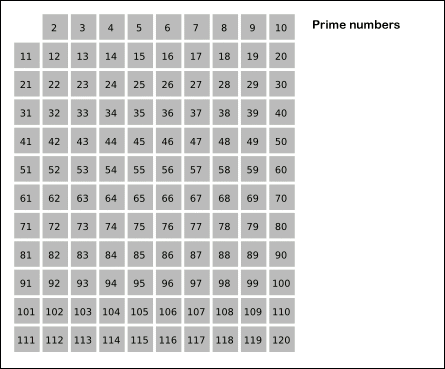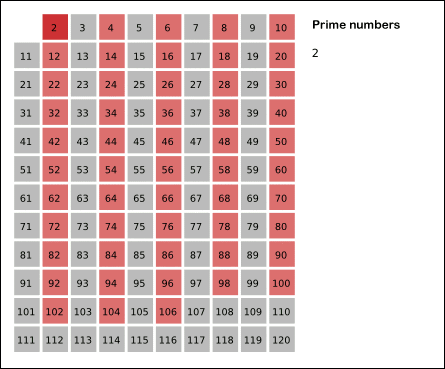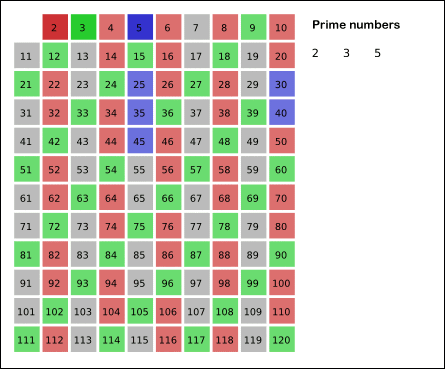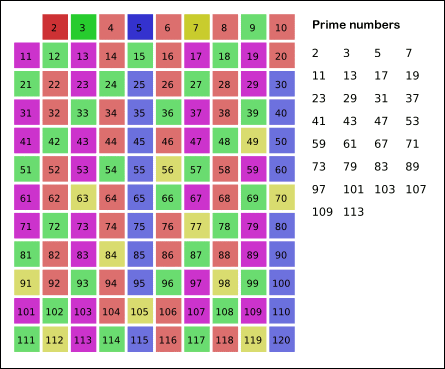
下面是本算法的实现代码：

const primesList = function(n) {
    let list = [];
    let signs = new Uint8Array(n);

    for (let i = 2; i < n; i++) {
        if (!signs[i - 1]) {
            list.push(i);

            for (let j = i * i; j <= n; j += i) {
                signs[j - 1] = true;
            }
        }
    }
    return list;
};
let result = primesList(100);
console.log("list: " + result);
console.log("count: " + result.length);

• 时间复杂度：O(n * loglog n)

• 空间复杂度：O(n)

参考资料：

• 埃拉托斯特尼筛法 — 维基百科